
Recursion is a programming pattern that helps in situations where a task can be naturally split into several tasks of the same kind, but simpler. Or when a task can be simplified into an easy action and a simpler variant of the same task.
A recursive function always has a condition to stop calling itself, otherwise, it will call itself indefinitely. So a recursive function typically looks like the following:
🔗Syntax
jsxfunction recurse() {if (condition) {// stop calling itself//...} else {recurse();}}
🔗Example
Let's learn recursion with a one simple example for better understanding
- The example i’m going to use is
factorial - So first let’s see what is
factorialthis is not a part of recursion We are going to just understand concept of factorial before we look at the example of factorial in recursion - What Is Factorial? :- The factorial of a number is the function that multiplies the number by every natural number
- Let’s see we have number 4 factorial what this translate to is
4 * 3 * 2 * 1=24so The factorial of4 is 24
Now let’s write a recursion function for factorial of 4 to find out the factorial of 4
jsxfunction factorial(n) {if (n == 1) {return 1;} else {return n * factorial(n - 1);// n * factorial(n - 1) is nothing just a factorial formula n! = n × (n - 1)!}}console.log(factorial(4)); // 24
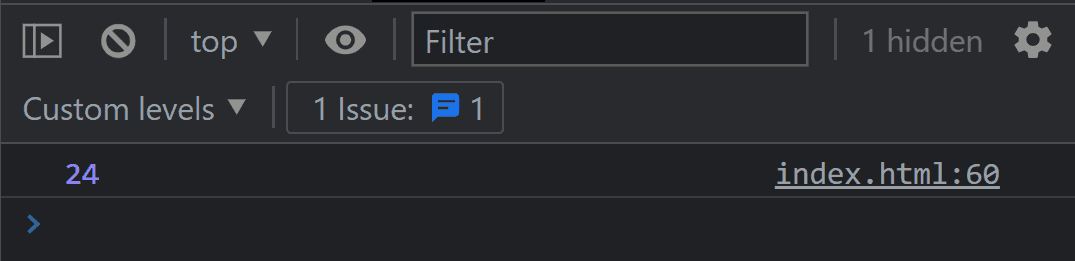
Behind the scene of above code 👇

